之前面试时遇到一个算法题:

假定两个矩形各条边都是平行于坐标轴，已知k、l、m、n分别为其中一个矩形左下角和右上角x轴、y轴坐标，p、q、r、s分别为另一个矩形的左下角和右上角x轴、y轴坐标，求这两个矩形的总面积，当矩形相交时要减去相交的面积。

此题利用常规的枚举法很复杂，但利用排除法和归纳法却能很快解决，故先记录下。

很明显，此题的重点在于如何判断矩形是否相交以及检测相交形成的新矩形面积，当不相交时总面积直接为两个矩形的面积之和，当相交时需要减去相交矩形的面积，由于题目已经告诉了矩形的左下角和右上角坐标已知，问题又转化为在相交时如何计算相交矩形的左下角和右上角的坐标。

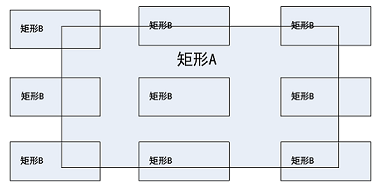
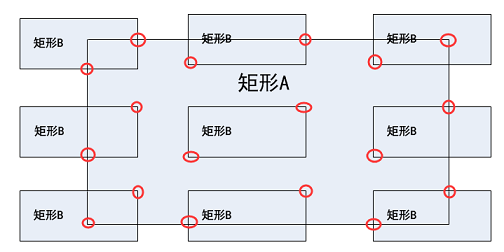
最开始我想通过常规的枚举法把矩形相交的所有情况都列出来，在稿纸上简单的比划后，发现采用枚举的方式太复杂，矩形相交理论上有下图所示的16种组合方式，短时间内很难一一列举出来，实际编程中不仅代码量大还很容易产生遗漏:

  • 两个矩形边角相交以及完全包含

    矩形相交1

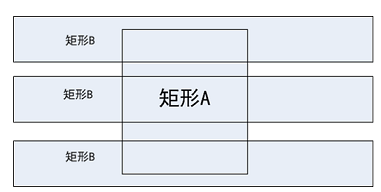
  • 矩形横向相交

    矩形相交2

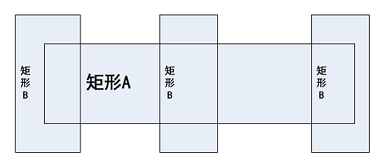
  • 矩形纵向相交

    矩形相交3

  • 矩形被完全包含

    矩形相交4

排除枚举方法之后，只能对其进行分析找出通用的处理方式。下图展示了在相交矩形的左下角和右上角的位置，仔细分析后便可发现相交矩形的左下角x,y坐标是两个矩形左下角x,y坐标中取较大值，相交矩形的右上角x,y坐标是两个矩形右上角x,y坐标中取较小值。
矩形相交坐标计算
通过分析归纳之后，我们将之前的16种相交情况统一为1个表达式，而这个表达式在编程时是很容易实现的，下面的代码展示了如何利用该表达式计算相交矩形的坐标以及其面积。

public static int calculateIntersectArea(int k, int l, int m, int n, int p,int q, int r, int s) {
	int leftDownX = 0, leftDownY = 0, rightUpX = 0, rightUpY = 0;
	leftDownX = k > p ? k : p;
	leftDownY = l > q ? l : q;
	rightUpX = m < r ? m : r;
	rightUpY = n < s ? n : s;
	return (rightUpX - leftDownX) * (rightUpY - leftDownY);
}

寻找出如何计算相交矩形的面积之后，还需要解决一个问题:上述实现只有在矩形相交时才正确，当矩形不相交时计算结果错误，为此需要找出一个方法判定两个矩形是否相交。若利用枚举方法同样会有前述的16种情形需要考虑，同样很复杂，显然枚举方法不适合使用。换一种思路：如果把矩形不相交的情形排除掉，那么剩下的情形就是矩形相交了！，而矩形不相交则相对容易多了，假设这两个矩形分别为A和B，则它们不相交一共有如下图所示的4种情况：
矩形不相交坐标计算
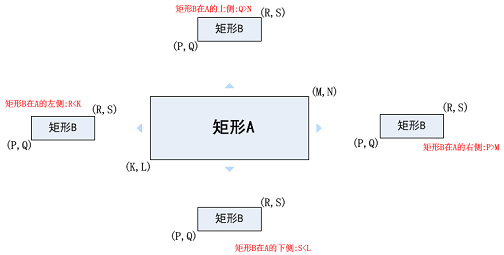
相应的代码实现如下：

public static boolean isIntersect(int k, int l, int m, int n, int p, int q, int r, int s) {
	
	boolean nointersect = false;
	// B在A的上面
	nointersect = q > n;
	// B在A的下面
	nointersect = l > s;
	// B在A的左侧
	nointersect = r < k;
	// B在A的右侧
	nointersect = m < p;

	return !nointersect;
}

利用上述2个判断方法，可以方便准确的计算出两个矩形在相交时的总面积，相应的代码如下:

public static int solution(int k, int l, int m, int n, int p, int q, int r, int s) {

	int widthA = m - k;
	int heightA = n - l;
	int areaA = widthA * heightA;

	int widthB = r - p;
	int heightB = s - q;
	int areaB = widthB * heightB;
	int totalArea = areaA + areaB;

	boolean hasIntersect = isIntersect(k, l, m, n, p, q, r, s);
	if (hasIntersect) {
		totalArea -= calculateIntersectArea(k, l, m, n, p, q, r, s);
	}
	return totalArea;
}

分析解决这个问题给我最深的感触是：有时候若某一类问题用枚举实现很复杂时，尝试去分析其中的规律，找出通用的解决方法，不仅在算法方面，或许在生活中其它方面也适用吧！